Table of Contents:
- Introduction
- Foundation of Neural Networks
- Activation Functions – Impact
- Role of Hidden Layers, Neurons and Weights
- Mathematics behind Neural Networks
- Optimizers and Transfer Learning
- Key Images Gallery
- Final Thoughts
InnoQuest Cohort-1 has been an enlightening journey, and the session on Neural Networks as Classifiers was no exception. Delivered by my favorite mentor, Dr. Ahmed Raza Shahid, this class dived deep into the theoretical and mathematical workings of neural networks, providing clarity on several long-standing questions.
Exploring Neural Networks and Their Foundations
Dr. Ahmed began the lecture by explaining the fundamentals of neural networks, drawing parallels to how human neurons operate. This was followed by an introduction to artificial neurons, detailing their role in Artificial Neural Networks (ANNs). Despite my prior exposure to the topic through courses by Krish Naik and CampusX, the session provided new insights, especially on the relationship between Machine Learning (ML) and Deep Learning (DL) in training models.
How do ML and DL intersect?
Previously, I had struggled to fully grasp how ML and DL intersect, especially regarding training. Dr. Ahmed’s explanation helped clarify that:
- In ML, algorithms like Linear Regression, Logistic Regression, and Support Vector Machines (SVM) use hyperplanes to solve problems. However, they are limited to one hyperplane, even in multi-dimensional spaces. When the data becomes more complex, ML algorithms change their approach—such as using tree structures (e.g., Decision Trees or Ensemble Techniques) or proximity-based methods (e.g., KNN)—but they do not draw multiple hyperplanes within any single algorithm.
- In DL, each neuron in a network functions like an ML algorithm, but with the advantage of drawing multiple hyperplanes via a network of neurons. This enables solving non-linearly separable problems, which ML struggles with.
After this lecture, I revisited TensorFlow Playground to apply my understanding of hidden layers, the job of neurons, and weights. This time, I designed networks capable of solving even the most complex problems much faster and with fewer epochs, solidifying these concepts through hands-on experimentation.
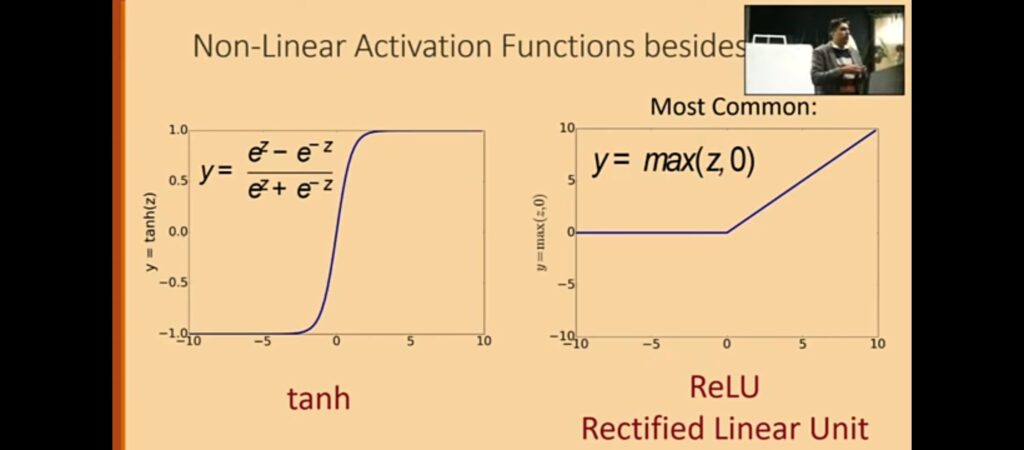
Activation Functions and Their Impact
The session also covered activation functions, exploring their influence on learning and convergence. Key takeaways included:
- Sigmoid: Covered in an earlier lecture, it introduces non-linearity but can saturate gradients.
- Tanh: Provides steeper gradients, improving convergence in some cases.
- ReLU: Simplifies training by setting negative inputs to zero, reducing computational cost.
We even touched upon advanced functions like Leaky ReLU and ELU, which mitigate ReLU’s drawbacks.
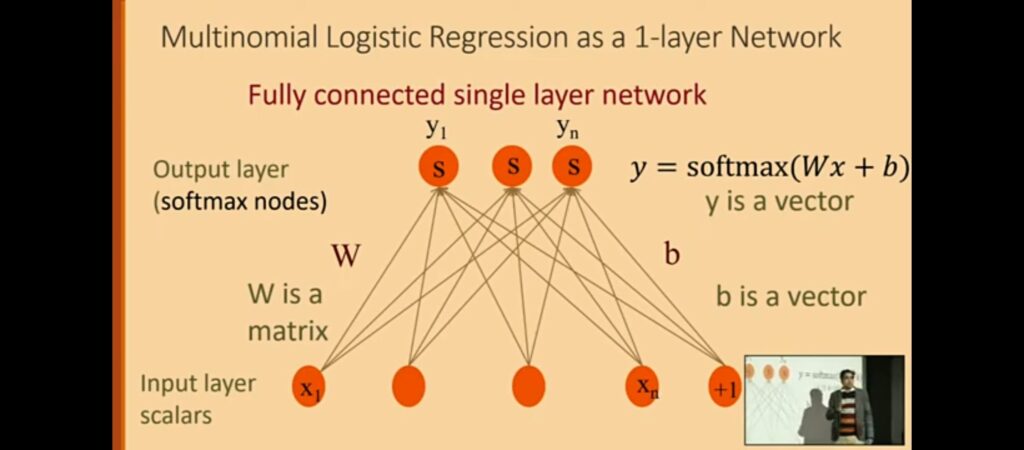
Role of Hidden Layers, Neurons, and Weights
One of the most valuable insights was understanding the role of hidden layers in ANNs. Dr. Ahmed explained that:
- Neurons primarily draw hyperplanes to separate data.
- Hidden layers project data into new dimensions, making it easier for neurons to find these hyperplanes.
- Weights act as templates learned by the network to recognize features.
A glimpse into Convolutional Neural Networks (CNNs) further reinforced this concept, showcasing how kernels (templates) identify patterns in images. This analogy helped bridge my understanding of weights as templates in both CNNs and ANNs.
Mathematics Behind Neural Networks
The class delved deep into the mathematics of ANNs, including:
- Forward propagation and backward propagation using the chain rule.
- The importance of the computation graph, which enables parallel processing in libraries like TensorFlow.
While I’m still refining my understanding of these concepts, the lecture provided a solid foundation for further exploration.
Optimizers and Transfer Learning
The session concluded with a discussion on optimizers, including:
- Momentum Optimizer: Accelerates training by overcoming saturation areas.
- RMS Prop: Uses adaptive learning rates for better generalization.
- Adam Optimizer: Combines momentum and adaptive learning for optimal performance.
We also touched on transfer learning, using real-world examples to illustrate its practical applications.
Image Gallery






Final Thoughts
This class was a transformative learning experience. It not only enhanced my theoretical knowledge of neural networks but also deepened my understanding of their mathematical working. Concepts like hidden layers, activation functions, and optimizers now feel more intuitive.
I look forward to building on these insights and exploring the vast potential of neural networks in solving complex problems.
